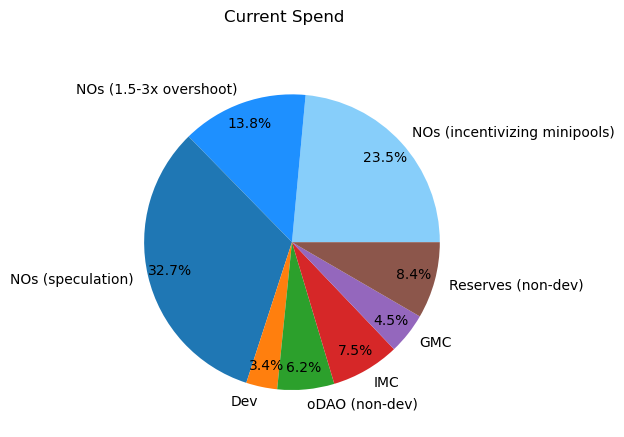
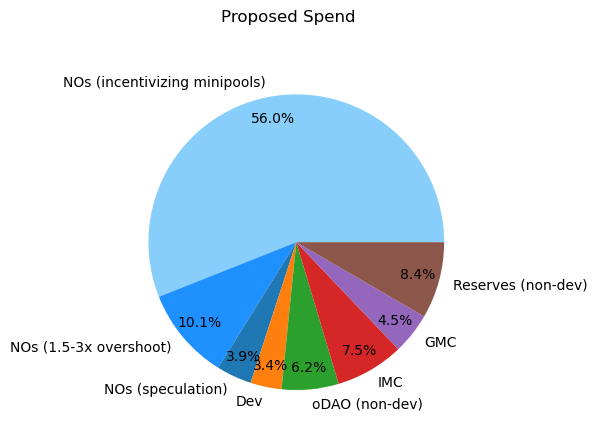
In defense of simplicity:
I’m going to make the argument that the logarithmic structure will not affect behavior in any predictable way because the incentives will not be in any way predictable to a human. A linear system will be superior.
This bracketed linear system roughly matches the marginal effectiveness/curve of the proposed rules
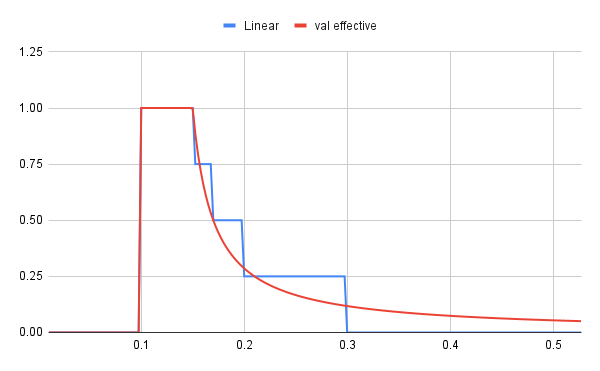
This curve is
if pETHratio<0.1, total effective RPL = 0. Otherwise, for all RPL <0.15 pETH, effectiveness is 100%, for 0.15-0.17, effectiveness is 75%, for 0.17-0.20, effectiveness is 50%, for 0.2-0.3, effectiveness is 25%; beyond 0.3, effectiveness is 0%.
It’s fairly obvious from the linear graph and the equation what your marginal effectiveness or APR is for any level of RPL. At some levels of collateral logarithmic provides better rewards, at others linear does.
Concerns with the logarithmic curve
We can match the logarithmic more accurately; for the 75% rule, this would mean RPL holders from 0.15-0.155 would do better on than linear, and 0.155-0.16 would do worse than linear. In comparing the two, that maximum decreased rewards for the linear discontinuity would be approximately 0.005[amount from .15-.155]/.015[amount of core 100% RPL]*.5[triangular area under the curve, decreases as you approach 0.155]*25%[decreased marginal effectiveness between curves]`, or about 0.417% of their RPL rewards for the month.
-
I think it is extremely unlikely that anyone except a bot will make an adjustment to their holdings based on improving rewards, at maximum, by less than one half of 1% of RPL rewards, or 0.2% of total rewards. So like 8.35% blended APR becomes 8.33%.
-
For every individual in the proposed rule who sells RPL/bond reduce because they are above the linear, there will be about as many people below the curve who would not sell RPL/bond reduce because they get more rewards (pETH ratio 0.155-.016). So whether one is more concerned about increasing the amount of rETH created or decreasing negative RPL action, it mostly won’t matter.
-
You have to have huge scale to even consider this proposition- because we are talking about selling chunks of 8 ETH of RPL to make a new minipool. If you are in the sweet spot (pETH ratio 0.1525) and have 100 8E minipools, then selling RPL to get another minipool would sink you to about .1477, well below the maximum efficiency of 0.15. So you’d have to have well north of 100 minipools to even bother making this calculation, so we are talking about maybe 1% of NOs maximum.
-
To me most compelling, is that it absolutely won’t matter what someone chooses to do this month, because the volatility of RPL is far greater than 1.5% per month. So if you have someone who would buy at 0.1525, but not at 0.155, they are 50% likely to sell the next month when ratio >.155; and if they would sell at 0.1525 but not at 0.150, they are 50% likely to buy the next month when ratio <0.15. In other words, the pETH ratio volatility greatly outstrips any possible decisions one might make within the critical 0.15-0.16 range. All we may possibly be doing with a granular reward system is encouraging node operators to buy and sell every month to hit some specific target (ie, increase churn).
A simile scenario (this is mostly fluff, you can skip it):
Comparisons are often strawman arguments- hopefully this is not, but i’d welcome critiques to make it less strawman-ish.
You make 40$/hr. You need childcare and want to hire a babysitter who costs 20$/hr. Great, you hire them!
But wait, you also decide your time with your flesh and blood is worth 10$ an hour. But 20+10 is still less than 40$ an hour. So hooray, you hire them.
But wait, you have to pay taxes. You have to pay 20% in taxes. Hooray, 20+10 is less than 40*0.8; you hire them!
But wait, this is a progressive tax. You estimate how much you will work this year- you fall into the 22% marginal tax bracket. You hire them! But you can tell by eyeballing that if you get any big bonuses at the end of the year, you’ll be pushed into the 30% marginal tax bracket. Which means you should stop working and stay home with the kids.
But wait, this is a logarithmic tax structure. You pull out your scientific calculator. After solving for ‘X’, you find that if you work up to 2100 hours this year, it will have been worth it to hire the babysitter; unless you get that bonus, then you can pull out your calculator and figure if it is worth it to stay home.
But wait, this logarithmic tax structure is also multiplied by the difference in year over year inflation. It was 4% last year. You pull out your scientific calculator and estimate that if it is more than 4% next year and you work under 2100 hrs, it’s worthwhile to get a babysitter. If it’s 3.5%, you can work 2400 hrs and still make it worthwhile to get a babysitter. But if it’s 4.5%, you should have only worked 1700 hrs before staying home with the kids. And if it hits 5%, then really after 1000 hrs you should stop working and just stay home with the kids. So you study some TA and get a copy of the economist and try to figure out what the current guess for next year’s inflation is before deciding on your child care options. And it’s very possible that if inflation is 6% next year you should just have stayed home the whole time.
This final scenario is my concern for how the tokenomics will work in practice. A finely granular structure of rewards requiring calculation with any small change, but where the calculation won’t generally help people make real world decisions because those decisions will be completely outstripped by a highly volatile metric (RPL/ETH ratio) that is outside their control.
Risks/benefits of a bracketed linear system
Risks:
- Rather than a smooth curve, there are discontinuities in linear systems with edge effects that will change people’s decisions.
notably, these are discontinuities in slope but not rewards. I believe that these are unlikely to affect human behavior based on my arguments above.
- There is no benefit for staking RPL beyond 0.3, suggesting people will be more prone to sell RPL which could affect RPL price.
While this is conceivable, at this point we would be talking about <1% RPL APR under Val’s proposal. i don’t think anyone would stake at that level because of the rewards given the volitility of RPL/ETH ratio.
- There is increased complexity with 5 different linear curves (0, 100%, 75%, 25%, 0%)
i think humans are well equipped to deal with tax brackets when they come in nice round numbers
Benefits:
- A human can tell the effect on their bottom line when bond reducing, staking, or withdrawing RPL with minimal mental math
- It is easy to explain in real terms to people on discord or documents
- there is no rewards going to highly overcollateralized NOs, these are directed back into the sweet spots. This is a minimal benefit.
Conclusion:
My opinion is that I just don’t think humans are capable of using something so granular as a logarithmic system to make real decisions. And I’m sure humans are not capable of successfully estimating future RPL/ETH ratio movements within 3% bands in a timeframe longer than a few days, at least not until we are much more mature as a protocol. If the incentives will not affect human behavior, then they are complexity without benefit. So consider a linear tiered reward system like the above. Or consider just a flat system, where we reward people to be in the sweet spot we want them to be in (let’s say just reward pETH ratio 0.10-0.20), and nothing else.